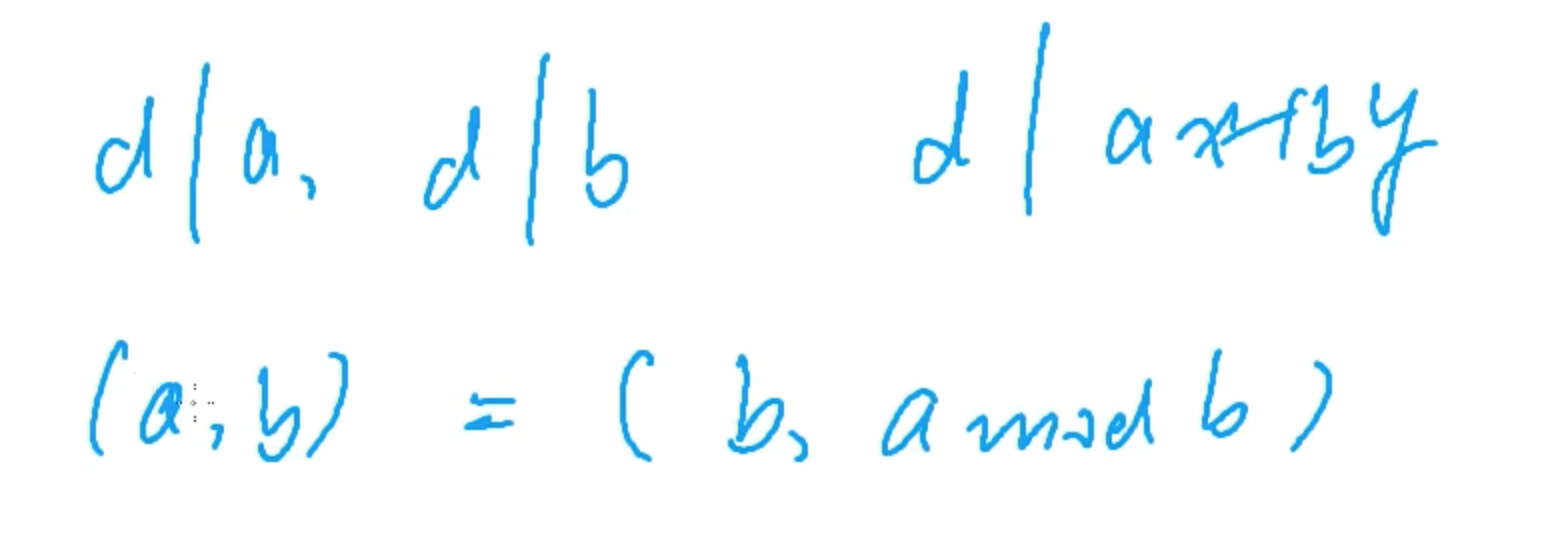算法基础课|数学知识|约数

发表于 分类于 浏览： 阅读时长 ≈ 1 分钟
ACWing 算法基础课笔记 约数相关

约数

试除法求约数

时间复杂度：O(sqrt(n))

约数也是成对出现，枚举每一对中较小的那一个，处理一下边界

1
2
3
4
5
6
7
8
def solve(n):
    res = []
    for i in range(1, int(n ** 0.5) + 1):
        if n % i == 0:
            res.append(i)
						# 9的约数是3 * 3 不能重复放进去 
            if i != n // i: res.append(n // i)
    return res

约数个数 & 约数的和

一个数N分解质因数，其约数个数为ans

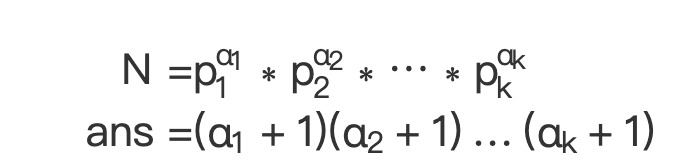
Untitled

比如 $2^5$的约数为（$2^0,2^1,2^2,2^3,..,2^5)$一共六个

Untitled

1
2
for k,v in dic.items():
    res = res * (v + 1) % MODE

计算约数的和时，可以使用 t = (t * p + 1)

1
2
3
4
5
for q, a in dic.items():
        t = 1
        for i in range(a):
            t = (t * q + 1) % MODE
        res = res * t % MODE

Untitled

最大公约数

时间复杂度： O(logn)

最大公约数（GCD）可以使用欧几里得算法（辗转相除法）求得。该算法的基本思想是不断用较小的数除以较大的数，直到两个数中有一个是0为止。此时，另一个非零的数就是最大公约数。

  • 性质一：如果d能够整除a，d能够整除b，那么d可以整除 a * x + b * y
  • 性质二：a和b的最大公约数(a, b)，等价于 (b, a mod b)

Untitled

Untitled